In this interview Diana Laurillard explains why constructionist principles are so valuable to education and how they can be incorporated into fun games that people want to play.

Diana is Professor of Learning with Digital Technologies at the UCL Knowledge Lab. She was previously Head of the E‑Learning Strategy Unit at Department for Education and Skills and Pro-Vice Chancellor for Learning Technologies at the Open University. Her research includes large-scale online communities of teacher-designers, and the use of specialised digital course design tools to enable teachers to create and share new pedagogies for using learning technology. She is currently running two MOOCs on teacher development in digital learning design.

There is a growing trend for researchers in the field of psychology to use games in their experiments. This interview is part of a series interviewing pioneers the field of gamified research who have used Gorilla to develop their experimental designs.

For what areas of research have you used Gorilla?

I got into looking at the neuroscience of education, I suppose, partly because my husband was working on dyscalculia as an interesting research field in neuroscience. I work at the other end of the spectrum in the classroom, in education with teachers and learners. With teachers of special needs, I had the chance to observe some of the difficulties that students have and one of them, for example, is that, although they can count, they can’t manipulate numbers. It’s almost as if they see the counting words as being a bit like the alphabet, a kind of arbitrary string of sounds. If I were to ask you what’s the relationship between the letter K and the letter P, you wouldn’t know what I was talking about. What do you mean, relationship? There isn’t one; it doesn’t make sense. For dyscalculia learners, you say what’s the relationship between the number 9 and the number 13 and it doesn’t mean a thing to them, because they don’t see numbers as being made up of other numbers.

How did you use games to help children with dyscalculia develop relationships between numbers?

What special needs teachers do is to introduce manipulation of objects. So you can have a set of three beads representing the number three, and then have to relate that to the digit 3. And then you have two beads relating to the digit 2, and you have to see that you can combine those to make five beads. So now you can see you’re bringing those two together, you count up how many there are, and you can relate it to the number. In the digital game, if you’re given a goal to make a set of five beads and you’ve got a play area where you’ve got ones, twos, threes, fours and sixes — you can either split these or you can put them together to try and make the goal of a set of five. So it’s about experiencing the relations between numbers in order to make a given number.

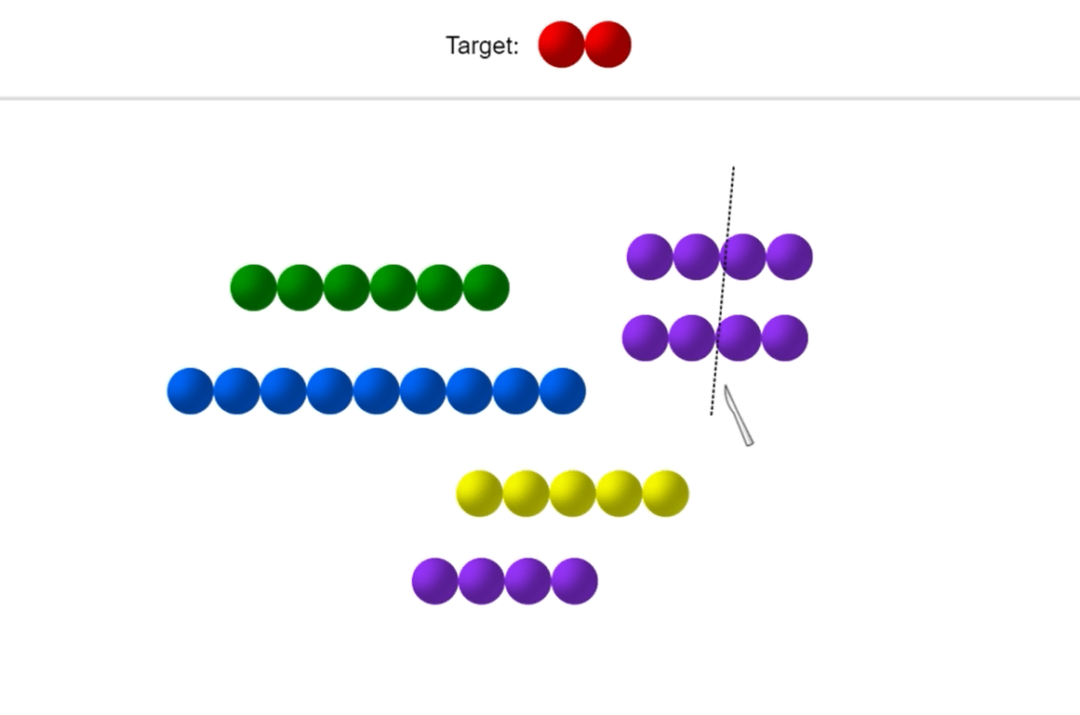
The fractions game we developed is similar. You have a rod of a particular length and you’ve got to make halves, and quarters and so on by using a virtual knife to divide it up. So you’ve got things you’ve got to try to construct by splitting or putting things together. In both cases, it’s giving the child a micro world which is behaving in a way that helps them learn about the behaviour of the objects in that world, a constructionist approach to learning.

Could you give us a bit more of an idea of what constitutes a constructionist game?

The principles are that you’re creating a world in which the conceptual nature of what you’re doing is represented in actions and transactions within that world. It’s not like having multiple choice questions when you say which of these combinations will make five and they pick one. They are actually constructing the goal themselves, so it’s a very different kind of learning experience. They’re never told they’re wrong, it’s just, ‘Whoops, I didn’t make that. Let me try again!’. The feedback is informational feedback in the way that you get informational feedback in the world. If you’re trying to kick a ball into a goal and it goes a bit too far to the right, you’ve got to angle your body in a different way. It’s that kind of immediate intrinsic feedback on your action in relation to a goal that helps you judge for yourself how to improve that action.

Could constructionist principles be applied to areas outside of mathematics, language for example?

Absolutely. You’ve got a lot of construction going on in making words out of syllables, sounds out of phonemes, graphemes which relate to phonemes, sentences that build from words and from clauses, and so on. There has certainly been work done on how to help children understand the relationship between graphemes and phonemes. For example, you might get a sound of a phoneme and you’ve got to identify which letters you have to put together to make your phoneme sound the same. Then you might use phonemes to make up a particular word sound that you’re given, and try to construct the right phonemes to match the sound. Things like that can certainly work for the context of language.

You mentioned that the purpose of creating a game for your intervention was to create a world which the child could manipulate, enabling constructionist learning. Did you consider using aspects of gamification to increase attention and motivation?

One of the principles we had right from the start was that we stripped down the visual aspects of the game as much as we possibly could to just the things you’ve got to focus on to get the conceptual idea. So there was no background, there were no pictures, there were no floppy bunnies or hopping frogs or anything else! There was also no virtual environment or the kinds of things that games typically have where you’re in a place and you’re doing something in that place. And the children were fine with it. In fact I remember one little guy who was talking to himself and the beads saying, “Okay, you red guys, you’ve got to come over here and meet these purple guys, And you’ve got to get together.” And then he said, “This is the best game ever.” He was contributing his own imagination for the context, and just got so excited by succeeding; that’s all they need.

There’s a lot of distraction in all that detail in the virtual game environment and I don’t think it’s necessary for children. Motivation should always be in trying to achieve this goal, and the goal should always be something which is conceptually driven. An awful lot of games make the goal extrinsic to the game itself, so you get some kind of reward if you’ve done the multiplication correctly or something. There’s no internal relationship between the reward and getting the multiplication right. For our constructionist games, the reward is matching the goal. That’s all there is to it and that’s how we learn in the world. The goal when you’re a toddler is to walk across the room without bumping into the chair and it’s satisfying when you manage it.

Are there any aspects of game design which you would like to be able to incorporate in the future?

Sometimes it’s good to get learners working together, so they’re deciding things together. One of them might say, “I think that’s an R”, and the other one, “No, I think it’s a P”, or something. Then they’ve got to listen to it again and come to an agreement. It’s a way of them motivating each other to listen more carefully. With collaborative learning, sometimes you can get more bangs for your buck.

You could also have a multiplayer approach. We had a design a while ago where there was one child who had to describe to the other what they had to do in order to build a tower. Only one child can do the construction but they can both see what happens. So the child giving the instructions knows if you haven’t made what they wanted to make. You can also have competitive games although we haven’t done that because there’s so much anxiety around with maths that you don’t want to increase it. But some kids love it anyway, so that could be another direction to take.

This interview is part of a wider series of interviews looking at gamified research. Make sure to follow this link to have a read through them!